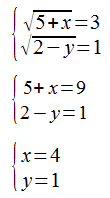Введение
Честно сказать, до жути надоело считать производные вручную, при том, что увы но при вычислении оных можно столько раз ошибиться, а для написания отчетов требуется именно вся запись в символьном виде. Конкретно от пакета Maxima лично меня интересуют производные, но не будем спешить рассмотрим все постепенно:
Установка
Для установки maxima, так как я пользователь Fedora 18 используем:
sudo yum install maxima
ну а под ubuntu и ей подобные:
sudo apt-get install maxima
Maxima, как калькулятор
Кто-то считает, с графическим интерфейсом лучше, лично я поставил wxmaxima так и не понял, как ей пользоваться, поэтому в дальнейшем используем консоль. Сразу скажу из недостатков консольного режима является, то что вводить нужно без ошибок, иначе удаляешь все и печатаешь по новой!
Теперь приступим к первому знакомству. Когда вы запустите Maxima вы увидите приглашение:
(%i1)
i - означает, что это приглашение на ввод, а цифра означает номер вычисления.
Maxima можно использовать, как калькулятор, правда
со странностями специфичный калькулятор:
(%i1) 1/4+2/3;
После того как закончили запись не забываем про символ ';', иначе вычисления так и не произойдут, пока вы не поставите, этот символ.
В результате получим:
11
(%o1) --
12
Как видим Maxima выдает результат после череды символов (%o1).
Maxima не любит иррациональности:
(%i2) (1 + sqrt(2))^5;
5
(%o2) (sqrt(2) + 1)
Для того, чтобы она это прорешала, используем функцию expand, а чтобы не повторять последний ввод, просто поставим символ '%':
(%i3) expand(%);
(%o3) 29 sqrt(2) + 41
Сразу предупрежу, вывод может отличаться, и это зависит от версии Maxima, главное, чтобы вывод при следующем шаге совпадал.
Следующим шагом будет вычисление численного значения:
(%i4) %,numer;
(%o4) 82.01219330881976
Согласен, это несколько неудобно. Что для вычислений требуется еще что-то писать, поэтому я и написал, что это весьма специфичный калькулятор.
Число можно вывести в научном формате:
(%i5) bfloat(%o4);
(%o5) 8.201219330881976b1
В данном примере мы выводим в научном формате значение полученное в четвертом вычислении на выходе %o4.
Точность выводимого значения можно менять с помощью функции. Например сделаем вывод в 5 знаков:
Теперь снова выведем значение в научном формате:
(%i7) ''%i5;
(%o7) 8.2012b1
В данном случае, чтобы повторить ввод, перед %i5 ставим два апострофа подряд.
Теперь побалуем с алгебраическими выражениями:
(%i1) (a+b)^2;
2
(%o1) (b + a)
Как видим ничего не произошло и опять требуется expand(), для того, чтобы добиться от Maxima, того чего желаем:
(%i2) expand(%);
2 2
(%o2) b + 2 a b + a
Мы можем подставить значение в уже записанное ранее выражение:
(%i3) %o2, a = 3/d;
6 b 9 2
(%o3) --- + -- + b
d 2
d
Что на мой взгляд является весьма удобной возможностью, учитывая остальные неудобности Maxima. Как видим сама по себе к общему знаменателю, она приводить не хочет, для этой цели воспользуемся функцией ratsimp:
(%i4) ratsimp(%);
2 2
b d + 6 b d + 9
(%o4) -----------------
2
d
Теперь воспользуемся функцией, factor, которая умеет выносить общие множители за скобки, а также распознавать многочлены в n-й степени:
(%i5) factor(%);
2
(b d + 3)
(%o5) ----------
2
d
Нелинейные алгебраические уравнения
Также Maxima умеет решать нелинейные алгебраические уравнения. Для примера взял уравнения которые выдал гугль по запросу нелинейные алгебраические уравнения:
Решим данную систему в Maxima:
(%i6) x^2-x*y^2-y^2=19;
2 2 2
(%o6) - x y - y + x = 19
(%i7) x-y=7;
(%o7) x - y = 7
(%i8) solve([%o6,%o7],[x,y]);
(%o8) [[x = - 1.255641025641026, y = - 8.255641025641026],
[x = 5.620823620823621, y = - 1.379176755447942],
[x = 9.634816753926701, y = 2.634817813765182]]
Тригонометрия
Теперь побалуем с тригонометрией, первый пример я рассмотрю из мануала, потом парочку своих:
(%i9) sin(u+v)*cos(u)^3;
3
(%o9) cos (u) sin(v + u)
Воспользуемся функцией trigexpand, чтобы избавиться синуса суммы:
(%i10) trigexpand(%);
3
(%o10) cos (u) (cos(u) sin(v) + sin(u) cos(v))
Также Maxima может преобразовать наше выражение в многочлен, в котором, не будет синусов и косинусов в степенях, а все они будут стоять одни одинешеньки. Лучше продемонстрирую на примере:
(%i11) trigreduce(%);
sin(v + 4 u) + sin(v - 2 u) 3 sin(v + 2 u) + 3 sin(v)
(%o11) --------------------------- + -------------------------
8 8
Теперь я побалую, а конкретно меня интересует, знает ли Maxima основное тригонометрическое тождество, для этого я воспользуюсь функцией trigsimp, которая упрощает выражения:
(%i12) sin(x)^2+cos(x)^2;
2 2
(%o12) sin (x) + cos (x)
(%i13) trigsimp(%);
(%o13) 1
А теперь продемонстрирую пример, где конкретно очень необходима функция trigexpand:
(%i14) cos(u+v)*cos(u)+sin(u+v)*sin(u);
(%o14) sin(u) sin(v + u) + cos(u) cos(v + u)
(%i15) trigexpand(%);
(%o15) cos(u) (cos(u) cos(v) - sin(u) sin(v))
+ sin(u) (cos(u) sin(v) + sin(u) cos(v))
(%i16) expand(%);
2 2
(%o16) sin (u) cos(v) + cos (u) cos(v)
(%i17) trigsimp(%);
(%o17) cos(v)
Вот так красиво, можно упростить большую замуту :).
Комплексные числа
Теперь поработаем с комплексными числами, мнимая единица в Maxima обозначается как %i:
(%i1) w:6+%i*k;
(%o1) %i k + 6
Найдем вещественную и мнимую части комплексного числа:
(%i2) realpart(%o1);
(%o2) 6
(%i3) imagpart(w);
(%o3) k
Запишем комплексное число в показательной форме:
(%i4) polarform(w);
2 %i atan(k/6)
(%o4) sqrt(k + 36) %e
Найдем значение модуля и аргумента комплексного числа:
(%i5) cabs(w);
2
(%o5) sqrt(k + 36)
(%i6) carg(w);
k
(%o6) atan(-)
6
Дифференцирование и интегрирование
Наконец-то настал черед производных!
Сначала простой пример, который меня очень взволновал, так как именно это я и искал, и нашел в Maxima:
(%i1) diff(phi(t),t);
d
(%o1) -- (phi(t))
dt
Мне очень часто приходится сталкиваться с тем, что значение числа неизвестно, а записать производную от этого числа нужно, а известно лишь, то что оно зависит от переменной t и Maxima позволяет такие переменные дифференцировать!
Теперь продифференцируем сложную функцию:
(%i2) S:1/cos(phi(t))^2;
1
(%o2) ------------
2
cos (phi(t))
(%i3) diff(S,t);
d
2 sin(phi(t)) (-- (phi(t)))
dt
(%o3) ---------------------------
3
cos (phi(t))
Теперь проинтегрируем полученное выражение.
(%i4) integrate(%,t);
1
(%o4) ------------
2
cos (phi(t))
Как мы видим, Maxima не записывает константы интегрирования, она сразу приравнивает их нулю :(.
Дополнительно продемонстрирую интегрирование парочки табличных интегралов:
(%i5) k:sin(t);
(%o5) sin(t)
(%i6) integrate(k,t);
(%o6) - cos(t)
(%i7) k:1/cos(t)^2;
1
(%o7) -------
2
cos (t)
(%i8) integrate(k,t);
(%o8) tan(t)
Разложение в ряд Тейлора
Очень часто, для упрощения расчетов, тригонометрические формулы разлаживают в ряд Тейлора. Разложим в ряд Тейлора функцию косинуса:
(%i1) k:sin(t);
(%o1) sin(t)
(%i2) taylor(k,t,0,5);
3 5
t t
(%o2)/T/ t - -- + --- + . . .
6 120
Функция taylor имеет четыре параметры, первый указывает, функцию, которую хотим разложить в ряд Тейлора, второй параметр переменная по степеням которой выполняем разлаживание функции в ряд Тейлора, а следующие два параметра отвечают за диапазон выводимых значений по степеням в нашем случае от степени 0 по 5-ю степень t.
Пределы
Также Maxima умеет вычислять пределы с помощью функции limit(<имя функции>,<имя переменной>,<к чему стремится переменная>):
(%i3) limit(k,t,0);
(%o3) 0
(%i4) limit(k,t,inf);
(%o4) ind
Решение дифференциальных уравнений
Чтобы записать дифференциальное уравнение перед функцией diff пишется символ апострофа. Запишем дифференциальное уравнение для пружины с грузом и решим его:
(%i1) m*diff(x(t),t,2)=c*x(t);
2
d
(%o1) m (--- (x(t))) = c x(t)
2
dt
(%i2) ode2(%o1,x(t),t);
Is c m positive, negative, or zero?
positive;
sqrt(c) t sqrt(c) t
--------- - ---------
sqrt(m) sqrt(m)
(%o2) x(t) = %k1 %e + %k2 %e
Линейная алгебра
Теперь продемонстрирую простейшие операции с матрицами. Начнем с того, что введем матрицу:
(%i1) m: entermatrix (3, 3);
Is the matrix 1. Diagonal 2. Symmetric 3. Antisymmetric 4. General
Answer 1, 2, 3 or 4 :
4;
Row 1 Column 1:
a;
Row 1 Column 2:
b;
Row 1 Column 3:
c;
Row 2 Column 1:
d;
Row 2 Column 2:
e;
Row 2 Column 3:
f;
Row 3 Column 1:
g;
Row 3 Column 2:
h;
Row 3 Column 3:
k;
Matrix entered.
[ a b c ]
[ ]
(%o1) [ d e f ]
[ ]
[ g h k ]
Транспонируем ее:
(%i2) transpose(m);
[ a d g ]
[ ]
(%o2) [ b e h ]
[ ]
[ c f k ]
Вычислим обратную матрицу и проверим, действительно ли матрица является обратной:
(%i13) m1:invert(m),detout;
[ e k - f h c h - b k b f - c e ]
[ ]
[ f g - d k a k - c g c d - a f ]
[ ]
[ d h - e g b g - a h a e - b d ]
(%o13) ---------------------------------------------
a (e k - f h) + b (f g - d k) + c (d h - e g)
Здесь invert - функция инвертирования, а с помощью записи detout мы выносим за пределы определитель матрицы, чтобы запись была покороче. Вообще определитель матрицы находится с помощью функции determinant.
Теперь перемножим матрицу с обратной, для проверки:
(%i14) m.m1;
[ e k - f h c h - b k b f - c e ]
[ ]
[ f g - d k a k - c g c d - a f ]
[ a b c ] [ ]
[ ] [ d h - e g b g - a h a e - b d ]
(%o14) [ d e f ] . (---------------------------------------------)
[ ] a (e k - f h) + b (f g - d k) + c (d h - e g)
[ g h k ]
(%i15) expand(%);
a e k
(%o15) matrix([---------------------------------------------
a e k - b d k - a f h + c d h + b f g - c e g
b d k
- ---------------------------------------------
a e k - b d k - a f h + c d h + b f g - c e g
a f h
- ---------------------------------------------
a e k - b d k - a f h + c d h + b f g - c e g
c d h
+ ---------------------------------------------
a e k - b d k - a f h + c d h + b f g - c e g
b f g
+ ---------------------------------------------
a e k - b d k - a f h + c d h + b f g - c e g
c e g
- ---------------------------------------------, 0, 0],
a e k - b d k - a f h + c d h + b f g - c e g
a e k
[0, ---------------------------------------------
a e k - b d k - a f h + c d h + b f g - c e g
b d k
- ---------------------------------------------
a e k - b d k - a f h + c d h + b f g - c e g
a f h
- ---------------------------------------------
a e k - b d k - a f h + c d h + b f g - c e g
c d h
+ ---------------------------------------------
a e k - b d k - a f h + c d h + b f g - c e g
b f g
+ ---------------------------------------------
a e k - b d k - a f h + c d h + b f g - c e g
c e g
- ---------------------------------------------, 0],
a e k - b d k - a f h + c d h + b f g - c e g
a e k
[0, 0, ---------------------------------------------
a e k - b d k - a f h + c d h + b f g - c e g
b d k
- ---------------------------------------------
a e k - b d k - a f h + c d h + b f g - c e g
a f h
- ---------------------------------------------
a e k - b d k - a f h + c d h + b f g - c e g
c d h
+ ---------------------------------------------
a e k - b d k - a f h + c d h + b f g - c e g
b f g
+ ---------------------------------------------
a e k - b d k - a f h + c d h + b f g - c e g
c e g
- ---------------------------------------------])
a e k - b d k - a f h + c d h + b f g - c e g
(%i16) factor(%);
[ 1 0 0 ]
[ ]
(%o16) [ 0 1 0 ]
[ ]
[ 0 0 1 ]
Для матриц операция умножения выполняется с помощью оператора ".", при этом стоит помнить, что умножение a.b и b.a даст разные результаты! Это можно посмотреть в любом учебнике по линейной алгебре.
Найдем определитель матрицы и ранг матрицы:
(%i17) determinant(m);
(%o17) a (e k - f h) - b (d k - f g) + c (d h - e g)
(%i18) rank(m);
(%o18) 3
Чтобы найти собственные значения используется функция eigenvectors, при попытке вычислить оные от моей матрицы, передо мной появился дебагер ldb, видать буковки не особо нравятся функции eigenvectors :).
Поэтому продемонстрирую данную функцию на числовой матрице:
[ 1 2 3 ]
[ ]
(%o1) [ 4 5 6 ]
[ ]
[ 7 8 9 ]
(%i2) m:%;
[ 1 2 3 ]
[ ]
(%o2) [ 4 5 6 ]
[ ]
[ 7 8 9 ]
(%i3) eigenvectors(m);
3 sqrt(33) - 15 3 sqrt(33) + 15
(%o3) [[[- ---------------, ---------------, 0], [1, 1, 1]],
2 2
3/2
3 sqrt(33) - 19 3 sqrt(11) - 11
[[[1, - ---------------, - ------------------]],
16 8
3/2
3 sqrt(33) + 19 3 sqrt(11) + 11
[[1, ---------------, ------------------]], [[1, - 2, 1]]]]
16 8
Решение систем линейных алгебраических уравнений
Ну и напоследок, решим систему линейных алгебраических уравнений!
Опять нагуглил системку (так как лень готовить картинки, меня больше изучение Maxima колышет).
(%i14) A:matrix([100,6,-2],[6,200,-10],[1,2,100]);
[ 100 6 - 2 ]
[ ]
(%o14) [ 6 200 - 10 ]
[ ]
[ 1 2 100 ]
(%i15) B:matrix([200],[600],[500]);
[ 200 ]
[ ]
(%o15) [ 600 ]
[ ]
[ 500 ]
(%i16) X:invert(A).B;
[ 952900 ]
[ ------ ]
[ 499679 ]
[ ]
[ 1593300 ]
(%o16) [ ------- ]
[ 499679 ]
[ ]
[ 2457000 ]
[ ------- ]
[ 499679 ]
Запишем полученное значение в более приглядном человеческому глазу виде:
(%i17) X,numer;
[ 1.907024309606768 ]
[ ]
(%o17) [ 3.188647111445548 ]
[ ]
[ 4.917156814675021 ]
Второй способ решения данной СЛАУ, с помощью функции solve:
(%i41) D:[100*x+6*y-2*z=200,6*x+200*y-10*z=600,x+2*y+100*z=500];
(%o41) [- 2 z + 6 y + 100 x = 200, - 10 z + 200 y + 6 x = 600,
100 z + 2 y + x = 500]
(%i42) solve(D,[x,y,z]);
952900 1593300 2457000
(%o42) [[x = ------, y = -------, z = -------]]
499679 499679 499679
(%i43) %,numer;
(%o43) [[x = 1.907024309606768, y = 3.188647111445548, z = 4.917156814675021]]